哈希游戏- 哈希游戏平台- 哈希游戏官方网站

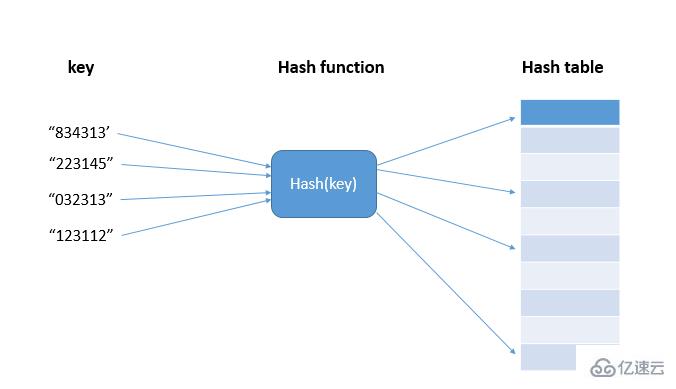
　　消息认证机制和数字签名机制都需要有产生认证符的基本功能，这一基本功能又作为认证协议的一个部分。 认证符是用于认证消息的数值，它的产生方法分为消息认证码(MAC, Message Authentication Code)和哈希函数(Hash function)两大类。 8.1消息认证码 消息认证码(MAC)是指消息被一密钥控制的公开函数作 用后产生的固定长度的数值。该数值作为认证符。也称为密码校验和。 用户A和用户B，共享密钥K； 发送方A对于消息M，计算MAC=CK(M)，其中CK(·)是密钥控制的公开函数，然后向B发送M MAC ； 接收方B收到M MAC后，做与A同样的计算，求得一个新的MAC，并与收到的MAC作比较，如图8.1(a)所示： 图8.1 MAC的基本使用方式 8.1消息认证码 8.1消息认证码 若仅收发双方知道K，且B计算得到的MAC与接收到的MAC一致，则该系统实现了以下功能： 接收者可以确信消息M未被篡改； 接收者可以确信消息来自所声称的发送者，即发送方不是冒充的； 如果消息中含有序列号，则可以保证正确的消息顺序。 注：MAC函数与加密算法类似，不同之处是MAC不必是可逆的，因此与加密算法相比更不容易被攻破。 8.1消息认证码 上述过程中，由于消息本身在发送过程中是明文形式，所以这一过程只提供认证性而未提供保密性。 为提供保密性可在MAC函数以后(如图8.1(b))或以前(如图8.1(c))进行一次加密，而且加密密钥也需被收发双方共享。 在图8.1(b)中，M与MAC链接后再被整体加密，在图8.1(c)中，M先被加密再与MAC链接后发送。 通常希望直接对明文进行认证，因此图8.1(b)所示的使用方式更为常用。 8.1消息认证码 考虑到MAC所存在的攻击类型，它应满足以下要求，其中假定敌手知道函数C，但不知道密钥K： ① 如果敌手得到M和CK(M)，则构造一满足CK(M′)=CK(M)的新消息M′在计算上是不可行的。 ② CK(M)在以下意义下是均匀分布的： 随机选取两个消息M、M′，Pr[CK(M)=CK(M′)]=2-n，其中n为MAC的长。 ③ 若M′是M的某个变换，即M′=f(M)，例如f为插入一个或多个比特，那么Pr[CK(M)=CK(M′)]= 2-n。 8.1消息认证码 第1个要求是说敌手不需要找出密钥K而伪造一个与截获的MAC相匹配的新消息在计算上是不可行的。 第2个要求是说敌手如果截获一个MAC，则伪造一个相匹配的消息的概率为最小。 最后一个要求是说函数C不应在消息的某个部分或某些比特弱于其他部分或其他比特，否则敌手获得M和MAC后就有可能修改M中弱的部分，从而伪造出一个与原MAC相匹配的新消息。 数据认证算法 数据认证算法是最为广泛使用的消息认证码中的一个，已作为FIPS Publication（FIPS PUB 113）并被ANSI作为X9.17标准。 算法基于CBC模式的DES算法，其初始向量取为零向量。需被认证的数据（消息、记录、文件或程序）被分为64比特长的分组D1，D2，…，DN，其中最后一个分组不够64比特的线，然后按以下过程计算数据认证码（见图8.2）： 数据认证算法 数据认证算法 其中E为DES加密算法，K为密钥。 数据认证码取为ON或者ON 的最左M个比特，其中16≤M≤64。 8.2 哈希函数 哈希函数H是一公开函数，用于将任意长的消息M映射为较短的、固定长度的一个值H(M)，作为认证符，称函数值H(M)为哈希值、杂凑值、杂凑码或消息摘要。杂凑码是消息中所有比特的函数，因此提供了一种错误检测能力，即改变消息中任何一个比特或几个比特都会使杂凑码发生改变。 可将MAC看成是带密钥的哈希函数。MAC主要用于保证消息的完整性。 哈希函数常用于数字签名。 图8.3 表示哈希函数用来提供消息认证的基本使用方式，共有以下6种： ① 消息与哈希值链接后用单钥加密算法加密。由于所用密钥仅为收发双方A、B共享，因此可保证消息的确来自A并且未被篡改。同时还由于消息和哈希值都被加密，这种方式还提供了保密性，见图8.3(a)。(提供认证性和保密性) ② 用单钥加密算法仅对哈希值加密。这种方式用于不要求保密性的情况下，可减少处理负担。注意这种方式和图8.1(a)的MAC结果完全一样，即将EK[H(M)]看作一个函数，函数的输入为消息M和密钥K，输出为固定长度，见图8.3(b)。(提供认证性) ③ 用公钥加密算法和发送方的秘密钥仅加密哈希值。和②一样，这种方式提供认证性，又由于只有发送方能产生加密的哈希值，因此这种方式还对发送方发送的消息提供了数字签字，事实上这种方式就是数字签字，见图8.3(c)。(提供认证性和数字签字) ④ 消息的哈希值用公钥加密算法和发送方的秘密钥加密后与消息链接，再对链接后的结果用单钥加密算法加密，这种方式提供了保密性和数字签字，见图8.3(d)。(提供认证性、数字签字和保密性) ⑤ 使用这种方式时要求通信双方共享一个秘密值S，A计算消息M和秘密值S链接在一起的哈希值，并将此哈希值附加到M后发往B。因B也有S，所以可重新计算哈希值以对消息进行认证。由于秘密值S本身未被发送，敌手无法对截获的消息加以篡改，也无法产生假消息。这种方式仅提供认证，见图8.3(e)。 ⑥ 这种方式是在⑤中消息与哈希值链接以后再增加单钥加密运算，从而又可提供保密性，见图8.3(f)。 由于加密运算的速度较慢，代价较高，而且很多加密算法还受到专利保护，因此在不要求保密性的情况下，方式②和③将比其他方式更具优势。 哈希函数应满足的条件 哈希函数的目的是为需认证的数据产生一个“指纹”。 为了能够实现对数据的认证，哈希函数应满足以下条 件： ① 函数的输入可以是任意长。 ② 函数的输出是固定长。 ③ 已知x，求H(x)较为容易，可用硬件或软件实现。 ④ 已知h，求使得H(x)=h的x在计算上是不可行的，这一性质称为函数的单向性，称H(x)为单向哈希函数。 ⑤ 已知x，找出y(y≠x)使得H(y)=H(x)在计算上是不可 行的。 如果单向哈希函数满足这一性质，则称其为弱单向哈希函 数。 ⑥ 找出任意两个不同的输入x、y，使得H(y)=H(x)在计 算上是不可行的。 如果单向哈希函数满足这一性质，则称其为强单向哈希函 数。 第⑤和第⑥个条件给出了哈希函数无碰撞性的概念，如果 哈希函数对不同的输入可产生相同的输出，则称该函数具 有碰撞性。 以上6个条件中，前3个是哈希函数能用于消息认证的基本要求。 第4个条件（即单向性）则对使用秘密值的认证技术(见图8.3(e))极为重要。假如哈希函数不具有单向性，则攻击者截获M和C=H(S‖M)后，求C的逆S‖M，就可求出秘密值S。 第5个条件使得敌手无法在已知某个消息时，找到与该消息具有相同哈希值的另一消息。这一性质用于哈希值被加密情况时(见图8.3(b)和图8.3(c))防止敌手的伪造，由于在这种情况下，敌手可读取传送的明文消息M，因此能产生该消息的哈希值H(M)。 但由于敌手不知道用于加密哈希值的密钥，他就不可能既伪造一个消息M，又伪造这个消息的哈希值加密后的密文EK[H(M)]。 然而，如果第5个条件不成立，敌手在截获明文消息及其加密的哈希值后，就可按以下方式伪造消息：首先求出截获的消息的哈希值，然后产生一个具有相同哈希值的伪造消息，最后再将伪造的消息和截获的加密的哈希值发往通信的接收方。 第6个条件用于抵抗生日攻击。 生日攻击 1. 相关问题 已知一杂凑函数H有n个可能的输出，H(x)是一个特定的输出，如果对H随机取k个输入，则至少有一个输入y使得H(y)=H(x)的概率为0.5时，k有多大？ (称对杂凑函数H寻找上述y的攻击为第Ⅰ类生日攻击。) k ≈ n/2。 特别地，如果H的输出为m比特长，即可能的输出个数n=2m，则k ≈ 2m-1。 在k个人中,找一个与某人生日相同的人的概率超过0.5时,k至少有多大? k=183. 生日攻击 2. 生日悖论 生日悖论是考虑这样一个问题：在k个人 中至少有两个人的生日相同的概率大于0.5 时，k至少多大？ k=23。 将生日悖论推广为下述问题：已知一个在1到n之间均匀分布的整数型随机变量，若该变量的k个取值中至少有两个取值相同的概率大于0.5，则k至少多大？ k=1.18*n1/2 ≈n1/2 3. 生日攻击 生日攻击是基于下述结论：设杂凑函数H 有2m个可能的输出（即输出长m比特），如果H 的k个随机输入中至少有两个产生相同输出的概 率大于0.5，则 k ≈ 2m/2. (称寻找函数H的具有相同输出的两个任意输 入的攻击方式为第Ⅱ类生日攻击。) 杂凑函数输出长度n应足够大，以防止生日攻击。 64-bits 认为太小。 通常 128-512bits。 目前使用的大多数杂凑函数如MD5、SHA，其结构都是迭代型的，如图8.4所示。 其中函数的输入M被分为L个分组Y0,Y1,…,YL-1，每一个分组的长度为b比特，最后一个分组的长度不够的话，需对其做填充。 最后一个分组中还包括整个函数输入的长度值，这样一来，将使得敌手的攻击更为困难，即敌手若想成功地产生假冒的消息，就必须保证假冒消息的杂凑值与原消息的杂凑值相同，而且假冒消息的长度也要与原消息的长度相等。 算法的核心技术是设计无碰撞的压缩函数f，而敌手对算法的攻击重点是f 的内部结构，由于f 和分组密码一样是由若干轮处理过程组成，所以对f 的攻击需通过对各轮之间的位模式的分析来进行，分析过程常常需要先找出f 的碰撞。由于f 是压缩函数，其碰撞是不可避免的，因此在设计f 时就应保证找出其碰撞在计算上是不可行的。 8.3 MD5杂凑算法 MD4是MD5杂凑算法的前身，由Ron Rivest于1990年10月作为RFC提出，1992年4月，改动很小的修订版以RFC 1320发表。 MD5 (RFC 1321) developed by Ron Rivest at MIT in 90’s. MD5算法描述 步骤1： 添加填充位(一个1和若干个0)。在消息的最后添加适当的填充位使得数据位的长度满足length ? 448 mod 512。即使消息长度已满足要求，仍需填充。例如，消息长为448比特，则需填充512比特，使其长度变为960。因此填充的比特数大于等于1而小于等于512。 步骤2： 添加长度。添加原始消息的长度（二进制位的个数），用64位表示。以小数在前的格式存储(即低位字节放在低地址字节上)。如果消息长度大于264，则以264为模数取模。 这样报文表示为L个512位的数据块：Y0,Y1,…,YL-1。其长度为L?512bits。令N=L?16,则长度为N个32位的字。(令M[0…N-1]表示以字为单位的消息表示) MD5算法描述 步骤3：初始化MD缓冲区。一个128位MD缓冲区用以保存中间和最终散列函数的结果。它可以表示为4个32位的寄存器(A,B,C,D)。 寄存器初始化为以下的16进制值： A = B = EFCDAB89 C = 98BADCFE D = MD5算法描述 步骤4：处理512位消息块（ 16个32位字）。压缩函数HMD5是本算法的核心。它包括4轮处理。4轮处理具有相似的结构,但每次使用不同的基本逻辑函数，记为F,G,H,I。每一轮以当前的512位数据块(Yq)和128位缓冲值ABCD作为输入，并修改缓冲值的内容。每次使用64元素表T[1…64]中四分之一的元素。 MD5算法描述 T表，由sin 函数构造而成。T的第i个元素表示为T[i]，其值等于 232?abs(sin(i)),其中i是弧度。由于abs(sin(i))是一个0到1之间的数，T表的每一个元素是一个可以表示成32位的整数。T表提供了随机化的32位模板，消除了在输入数据中的任何规律性的特征。 MD5算法描述 步骤5：输出结果。所有L个512位数据块处理完毕后，最后的结果就是128位消息摘要(杂凑值)。 CV0 = IV CVq+1 = SUM32(CVq,RFI[Yq,RFH[Yq,RFG[Yq,RFF[Yq,CVq]]]]) MD = CVL 其中， IV = ABCD的初始值（见步骤3）； Yq = 消息的第q个512位数据块； L = 消息中数据块数； CVq = 链接变量，用于第q个数据块的处理； RFx = 使用基本逻辑函数x的轮函数； MD = 最终消息摘要； SUM32 =对输入中每个字分别计算模232加。 MD5 压缩函数 压缩函数HMD5中有4轮处理过程，每轮对缓冲区ABCD进行16步 迭代运算，每一步的运算形式为： a?b + (( a + g(b,c,d) + X[k] +T[i])s) 其中， a,b,c,d = 缓冲区的4个字; g = 基本逻辑函数F,G,H,I之一； s = 对32位字循环左移s位，s的取值由表6-2给出。 X[k] = M[q?16 + k] = 在第q个512位数据块中的第k个32位字 T[i] = 表T中的第i个32位字； + = 模 232的加； 在每一步运算完成后，再右循环一个字，得到这一步迭代的输出。 4轮处理过程分别使用不同的基本逻辑函数F、G、H、I，每个逻辑函数的输入为3个32比特的字，输出是一个32比特的字，其中的运算为逐比特的逻辑运算，即输出的第n个比特是3个输入的第n个比特的函数，函数的定义由表6.3给出，其中∧，∨，- ， 分别是逻辑与、逻辑或、逻辑非和异或运算，表6.4是四个函数的线轮处理过程中，每轮以不同的次序使用16个字，其中在第1轮以字的初始次序使用。第2轮到第4轮分别对字的次序i做置换后得到一个新次序，然后以新次序使用16个字。3个置换分别为： ?2(i)= (1+5i) mod 16 ?3(i)= (5+3i) mod 16 ?4(i)= 7i mod 16 MD5的安全性 MD4 MD4的设计目标（被MD5继承） 安全性：寻找两个具有相同杂凑值的消息在计算上是不可行的。 速度：32位体系结构下计算速度快. 简明与紧凑：算法描述简单且易于编程. 有利的小数在前的结构(Intel 80xxx, Pentium ) MD4与MD5的区别 MD4用3轮,每轮16 步；MD5用4轮,每轮16步； MD4中第1轮没有常量加，第2轮中每一步使用相同的常量加，第3轮的每一步使用另一个常量加；MD5中4轮64步每一步使用不同的常量T[i]； MD5用了四个基本逻辑函数，每轮使用一个；MD4用了三个，同样每轮使用一个； MD5中每一步要加上前一步的结果；MD4没有这个加法. 8.4 安全杂凑算法 安全杂凑算法SHA(Secure Hash Algorithm)由美国NIST设计，于1993年作为联邦信息处理标准（FIPS PUB 180）公布。SHA-0是SHA的早期版本，SHA-0被公布后，NIST很快就发现了它的缺陷，修改后的版本称为SHA-1，简称为SHA。SHA是基于MD4算法，其结构与MD4非常类似。 算法描述 算法的输入为小于264比特长的任意消息，分为512比特长的分组，输出为160比特长的消息摘要。算法的框图与图8.5一样，但杂凑值的长度和链接变量的长度为160比特。 算法的处理过程有以下几步： ① 对消息填充与MD5的步骤①完全相同。 ② 附加消息的长度与MD5的步骤②类似，不同之处在于以大数在前（big-endian)方式表示填充前消息的长度。即步骤①留出的64比特当作64比特长的无符号整数。 ③ 对MD缓冲区初始化算法使用160比特长的缓冲区存储中间结果和最终杂凑值，缓冲区可表示为5个32比特长的寄存器(A, B, C, D, E)，每个寄存器都以big-endian方式存储数据，其初始值分别为AB=EFCDAB89，C=98BADCFB，DE=C3D2E1F0。 ④ 以分组为单位对消息进行处理每一分组Yq都经一压缩函数处理，压缩函数由4轮处理过程（如图8.8所示）构成，每一轮又由20步迭代组成。4轮处理过程结构一样，但所用的基本逻辑函数不同，分别表示为f1,f2,f3,f4。每轮的输入为当前处理的消息分组Yq和缓冲区的当前值A,B,C,D,E，输出仍放在缓冲区以替代A,B,C,D,E的旧值，每轮处理过程还需加上一个加法常量Kt，其中0≤t≤79表示迭代的步数。80个常量中实际上只有4个不同取值，如表6.5所示，其中 为x的整数部分。 第4轮的输出（即第80步迭代的输出）再与第1轮的输入CVq相加，以产生CVq+1，其中加法是缓冲区5个字中的每一个字与CVq中相应的字模232相加。 ⑤ 输出消息的L个分组都被处理完后，最后一个分组的输出即为160比特的消息摘要。 步骤③到步骤⑤的处理过程可总结如下： CV0=IV; CVq+1=SUM32(CVq,ABCDEq); MD=CVL 其中IV是步骤③定义的缓冲区ABCDE的初值，ABCDEq是第q个消息分组经最后一轮处理过程处理后的输出，L是消息（包括填充位和长度字段）的分组数，SUM32是对应字的模232加法，MD为最终的摘要值。 SHA的压缩函数 如上所述，SHA的压缩函数由4轮处理过程组成，每轮处理过程又由对缓冲区ABCDE的20步迭代运算组成，每一步迭代运算的形式为（见图6.9） 其中A，B，C，D，E为缓冲区的5个字，t是迭代的步数（0≤t≤79），ft(B,C,D)是第t步迭代使用的基本逻辑函数，CLSs为左循环移s位，Wt是由当前512比特长的分组导出的一个32比特长的字（导出方式见下面），Kt是加法常量，+是模232加法。 基本逻辑函数的输入为3个32比特的字，输出是一个32比特的字，其中的运算为逐比特逻辑运算，即输出的第n个比特是3个输入的相应比特的函数。函数的定义如表6.6。表中∧,∨, －,分别是与、或、非、异或4个逻辑运算，函数的线） 下面说明如何由当前的输入分组（512比特长）导出Wt（32比特长）。前16个值（即W0,W1,…,W15）直接取为输入分组的16个相应的字，其余值（即W16,W17,…,W79）取为 见图6.10。 与MD5比较，MD5直接用一个消息分组的16个字作为每步迭代的输入，而SHA则将输入分组的16个字扩展成80个字以供压缩函数使用，从而使得寻找具有相同压缩值的不同的消息分组更为困难。 SHA与MD5的比较 由于SHA与MD5都是由MD4演化而来，所以两个算法极为相似。 1. 抗穷搜索攻击的强度 由于SHA和MD5的消息摘要长度分别为160和128，所以用穷搜索攻击寻找具有给定消息摘要的消息分别需做O(2160)和O(2128)次运算，而用穷搜索攻击找出具有相同消息摘要的两个不同消息分别需做O(280)和O(264)次运算。因此SHA抗击穷搜索攻击的强度高于MD5抗击穷搜索攻击的强度。 2. 抗击密码分析攻击的强度 由于SHA的设计准则未被公开，所以它抗击密码分析攻击的强度较难判断，似乎高于MD5的强度。 3. 速度 由于两个算法的主要运算都是模232加法，因此都易于在32位结构上实现。但比较起来,SHA的迭代步数(80步)多于MD5的迭代步数（64步），所用的缓冲区（160比特）大于MD5使用的缓冲区（128比特），因此在相同硬件上实现时，SHA的速度要比MD5的速度慢。 4. 简洁与紧致性 两个算法描述起来都较为简单，实现起来也较为简单，都不需要大的程序和代换表。 5. 数据的存储方式 MD5使用小数前方式，SHA使用大数在前方式。两种方式相比看不出哪个更具优势，之所以使用两种不同的存储方式是因为设计者最初实现各自的算法时，使用的机器的存储方式不同。 对SHA的攻击现状 图6.10 SHA分组处理所需的80个字的产生过程 CVL-1 CV1 IV = 初始值 CVi = 链接变量， Yi = 第i 个输入分组 f = 压缩函数 n = 杂凑值的长度 b = 输入分组的长度 迭代型杂凑函数的一般结构 b Y0 n f b Y1 n f b YL-1 n f n n CVL CV0=IV= initial n-bit value CVi=f(CVi-1, Yi-1) (1 ? i ? L) H(M) = CVL IV=CV0 图8.4 迭代型杂凑函数的一般结构 报文 K bits L?512 bits=N ?32bits 报文长度 (K mod 264) 100…0 Y0 512 bits Y1 512 bits Yq 512 bits YL-1 512 bits HMD5 IV 128 HMD5 CV1 128 HMD5 CVq 128 HMD5 CVL-1 128 512 512 512 512 128-bit 摘要 图8.5 MD5的算法框图 填充 (1 to 512 bits) 以小数在前的格式存储： Word A: 01 23 45 67 Word B: 89 AB CD EF Word C: FE DC BA 98 Word D: 76 54 32 10 F,T[1…16],X[i] 16 steps G,T[17…32],X[?2(i)] 16 steps H,T[33…48],X[?3(i)] 16 steps I,T[49…64],X[?4(i)] 16 steps + + + + A B C D A B C D A B C D A B C D CVq 128 32 Yq 512 CVq+1 128 + is mod 232 图8.6 单个 512-bit分组 的MD5 处理过程 图8.7 压缩函数中的一步迭代示意图 A B C D A B C D + + + CLSs + g X[k] T[i] by Ron Rivest at MIT 图8.8 SHA的分组处理框图 图8.9 SHA的压缩函数中一步迭代示意图南京航空航天大学网络研究室 * Hash函数 * 第8章 消息认证、哈希函数 被动攻击：获取消息的内容、业务流分析。 抗击被动攻击的方法：加密。 主动攻击：假冒、重放、消息的篡改、业务拒绝。 抗击主动攻击的方法：消息认证、数字签名等。 消息认证： 是一个过程，用以验证消息的真实性（的确是由它所声称的实体发来的）和完整性（消息未被篡改、插入、删除），同时还用于验证消息的顺序性和时间性（消息未被重排、重放、延迟）。 数字签名： 属认证技术，实现消息的不可否认性。 图8.2 数据认证算法 图8.3 哈希函数的基本使用方式 图8.3哈希函数的基本使用方式 图8.3哈希函数的基本使用方式