哈希游戏- 哈希游戏平台- 哈希游戏官方网站

　　哈希表（Hash Table）的应用近两年才在 NOI 中出现，作为一种高效的数据结 构，它正在竞赛中发挥着越来越重要的作用。 哈希表最大的优点，就是把数据的存储和查找消耗的时间大大降低，几乎可 以看成是常数时间；而代价仅仅是消耗比较多的内存。然而在当前可利用内存越 来越多的情况下，用空间换时间的做法是值得的。另外，编码比较容易也是它的 特点之一。 哈希表又叫做散列表，分为“开散列” 和“闭散列” 。考虑到竞赛时多数人 通常避免使用动态存储结构，本文中的“哈希表”仅指“闭散列” ，关于其他方面 读者可参阅其他书籍。

　　4.1 应用的简单原则 什么时候适合应用哈希表呢？如果发现解决这个问题时经常要询问： “某个元素是否在已知集合中？” ，也就是需要高效的数据存储和查找， 则使用哈希表是最好不过的了！那么，在应用哈希表的过程中，值得注意 的是什么呢？ 哈希函数的设计很重要。一个不好的哈希函数，就是指造成很多冲突 的情况，从前面的例子已经可以看出来，解决冲突会浪费掉大量时间，因 此我们的目标就是尽力避免冲突。前面提到，在使用“除余法”的时候， h(k)=k mod p ，p 最好是一个大素数。这就是为了尽力避免冲突。为什么 呢？假设 p=1000 ，则哈希函数分类的标准实际上就变成了按照末三位数 分类，这样最多 1000 类，冲突会很多。一般地说，如果 p 的约数越多， 那么冲突的几率就越大。 简单的证明：假设 p 是一个有较多约数的数，同时在数据中存在 q 满足 gcd(p,q)=d 1 ，即有 p=a*d , q=b*d, 则有 q mod p= q – p* [q div p] =q – p*[b div a] . ① 其中 [b div a ] 的取值范围是不会超过 [0， 的正整 b] 数。也就是说， [b div a] 的值只有 b1 种可能，而 p 是一个预先确定 的数。因此 ① 式的值就只有 b1 种可能了。这样，虽然 mod 运算之后 的余数仍然在 [0，p-1] 内，但是它的取值仅限于 ① 可能取到的那些值。 也就是说余数的分布变得不均匀了。容易看出， p 的约数越多，发生这 种余数分布不均匀的情况就越频繁，冲突的几率越高。而素数的约数是最 少的，因此我们选用大素数。记住“素数是我们的得力助手” 。 另一方面，一味的追求低冲突率也不好。理论上，是可以设计出一个 几乎完美，几乎没有冲突的函数的。然而，这样做显然不值得，因为这样 的函数设计很浪费时间而且编码一定很复杂，与其花费这么大的精力去设 计函数，还不如用一个虽然冲突多一些但是编码简单的函数。因此，函数 还需要易于编码，即易于实现。 综上所述，设计一个好的哈希函数是很关键的。而“好”的标准，就 是较低的冲突率和易于实现。 另外，使用哈希表并不是记住了前面的基本操作就能以不变应万变 的。有的时候，需要按照题目的要求对哈希表的结构作一些改进。往往一 些简单的改进就可以带来巨大的方便。 这些只是一般原则，真正遇到试题的时候实际情况千变万化，需要具 体问题具体分析才行。下面，我们看几个例子，看看这些原则是如何体现 的。

　　注意到两个程序的用时并不像我们期望的那样，总是哈希表快。设 哈希表的大小为 P . 首先，当规模比较小的时候（大约为 a 10% * P，这个数据仅仅是通 过若干数据估记出来的，没有严格证明，下同） ，第二种方法比哈希表快。 这是由于，虽然每次计算哈希函数用 O(1) 的时间，但是这个系数比较大。 例如这道题的 H(x)=x mod 15589 ，通过与做同样次数的加法相比较，测 试发现系数 12 ，因为 mod 运算本身与快速排序的比较大小和交换元 素运算相比，比较费时间。所以规模小的时候，O(N)（忽略冲突）的算法 反而不如 O(NlogN)。这一点在更复杂的哈希函数上会体现的更明显，因 为更复杂的函数系数会更大。 其次，当规模稍大 （大约为 15%*P a 85%*P） 的时候，很明显 哈希表的效率高。这是因为冲突的次数较少。 再次，当规模再大 （大约为 90%*P a P ）的时候，哈希表的效 率大幅下降。这是因为冲突的次数大大提高了，为了解决冲突，程序不得 不遍历一段都存储了元素的数组空间来寻找空位置。用白箱测试的方法统 计， 当规模为 13500 的时候， 为了找空位置， 线 次运算；而当规模为 15000 的时候，平均竟然高达 2000000 次运算，某 些数据甚至能达到 4265833 次。显然浪费这么多次运算来解决冲突是不合 算的，解决这个问题可以扩大表的规模，或者使用“开散列” （尽管它是 动态数据结构） 。然而需要指出的是，冲突是不可避免的。

　　如果关键字的位数比较多， 超过长整型范围而无法直接运 算，可以选择其中数字分布比较均匀的若干位，所组成的新的 值作为关键字或者直接作为函数值。 2.3 冲突处理 线性重新散列技术易于实现且可以较好的达到目的。令数组元素个数 为 S ，则当 h(k) 已经存储了元素的时候，依次探查 (h(k)i) mod S , i=1,2,3…… ， 直到找到空的存储单元为止 （或者从头到尾扫描一圈仍未发 现空单元，这就是哈希表已经满了，发生了错误。当然这是可以通过扩大 数组范围避免的） 。 2.4 支持运算 哈希表支持的运算主要有：初始化(makenull)、哈希函数值的运算 (h(x))、插入元素(insert)、查找元素(member)。 设插入的元素的关键字为 x ，A 为存储的数组。 初始化比较容易，例如

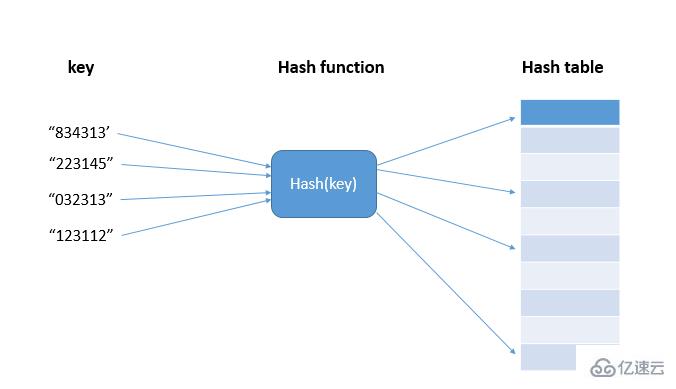
　　（哈希函数， 也叫做散列函数） ，使得每个元素的关键字都与一个函数值 （即数组下标）相对应，于是用这个数组单元来存储这个元素；也可以简 单的理解为，按照关键字为每一个元素“分类” ，然后将这个元素存储在 相应“类”所对应的地方。 但是，不能够保证每个元素的关键字与函数值是一一对应的，因此极 有可能出现对于不同的元素， 却计算出了相同的函数值， 这样就产生了 “冲 突” ，换句话说，就是把不同的元素分在了相同的“类”之中。后面我们 将看到一种解决“冲突”的简便做法。 总的来说， “直接定址”与“解决冲突”是哈希表的两大特点。 2.2 函数构造 构造函数的常用方法（下面为了叙述简洁，设 h(k) 表示关键字为 k 的元素所对应的函数值） ：